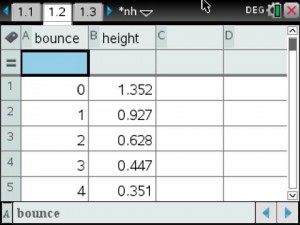
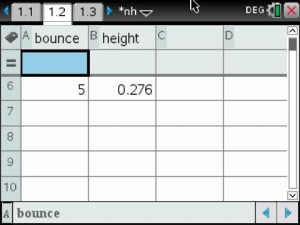
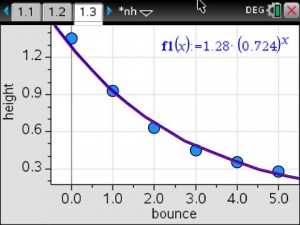
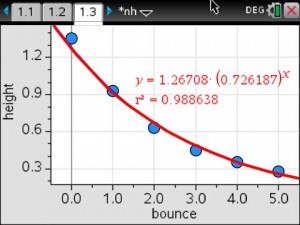
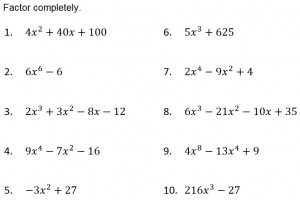Inspired by this post from Sarah Carter and this post from Kim Hughey, we played Ornaments on a Tree to review for our rational expressions exam.
Setup
I made two sets of trees (four trees per set). I put a point value on the back of each tree. I used 0 points, 2 points, 5 points, and -1 point. I also printed eight sets of problems (one per group) and put a colored sticker in the upper left corner. Then I laminated the trees and problems.
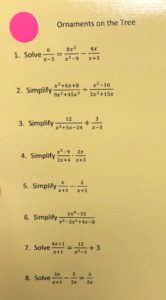
For each group, I wrote the numbers 1 – 8 on the colored stickers that would correspond to the group’s colored sticker.

Before class, I randomly taped a set of trees to the whiteboard. I put my desks in groups of four and gave each group four dry-erase boards and markers, an eraser, and the set of problems.
Playing the Game
Each person in the group must work the same problem. When every member of the group had all their work shown and an answer, the group would raise their hand so I could check their work and answer. If the group’s work and answers were correct, the group received a sticker. The color of the sticker matched the color of the sticker on their set of problems, and the number on the sticker indicated the problem they had correctly simplified or solved. One member of the group would then place the sticker on any one of the trees (not knowing what the point values were for the trees). Groups could work the problems in any order. Since I had numbered the stickers, I was able to keep track of which problems each group had already worked.
About 5 minutes before the end of the class, we stopped playing so that the points could be tallied.

Each sticker on the tree for each group was multiplied by the number of points on the back of the tree. The group with the highest point total was the winner and received a star sticker.
Since I had two sets of trees, I was able to run the game with back to back classes. In between classes, I removed the stickers from the previous class.